Centriole

** Definition, Function, Structure of Plant/Animal Cells


Definition: What is a Centriole?


Typically found in eukaryotic cells, centrioles are cylindrical (tube-like) structures/organelles composed of microtubules. In the cell, centrioles aid in cell division by facilitating the separation of chromosomes. For this reason, they are located near the nucleus.

Apart from cell division, centrioles are also involved in the formation of cilia and flagella and thus contribute to cell movement.

 

* While centrioles are typically found in eukaryotic cells, they are absent in higher plants. In these plants, then, cells do not use centrioles during cell division.




Centrioles can be found in:

 

  • Animal cells
  • Lower plants
  • Base of cilia and flagella (as basal bodies)

Diagram of a centriole by Kelvinsong [CC BY 3.0 (https://creativecommons.org/licenses/by/3.0)]Diagram of a centriole by Kelvinsong [CC BY 3.0 (https://creativecommons.org/licenses/by/3.0)]


Structure of Centrioles


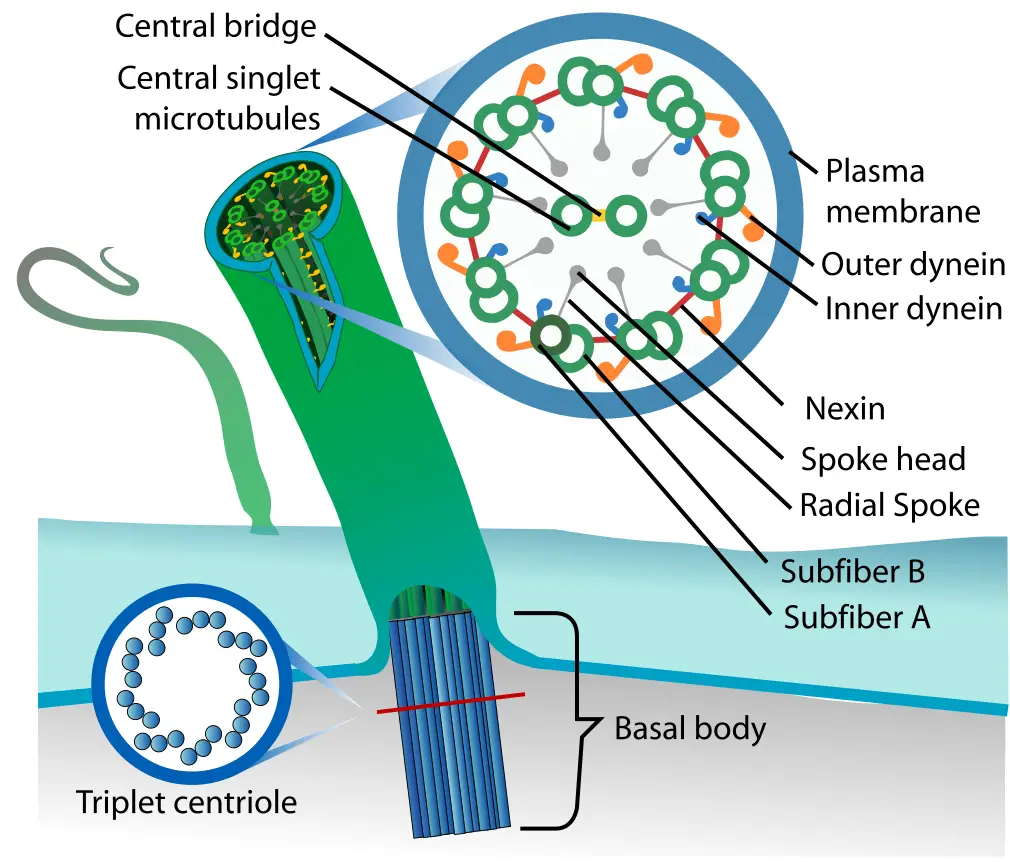
With a diameter of about 250nm and a length ranging from 150-500nm in vertebrates, centrioles are some of the largest protein-based structures. The nine triplets microtubules are some of the most recognizable features of this organelle.

In some organisms (e.g. in Drosophila and nematodes) the microtubules are simpler and may occur as either doublet microtubules (in flies) or single microtubules as is the case with Caenorhabditis elegans.

In human beings, however, among other higher animals, they exist as complex triplets that make up the scaffold of the microtubules arranged in a circle (at an angle) around the central core.

 

* When viewed from one end, the triplet microtubules appear to have an anticlockwise twist arrangement.


* At the ultrastructural level, the triplets of the structure are composed of 13 alpha and beta tubulins that contain protofilaments (A-tubule). Assembled in the protofilaments is a pair of 10 protofilaments microtubules known as B and C tubules.



Parts of a Centriole


Basically, the centriole is composed of three main parts. These include:


Distal Part


The distal part of the centrioles is characterized by the microtubules (triple or double). This part is also divided into the distal and sub-distal parts/appendages. While eukaryotic cells contain a total of nine distal appendages, sub-distal appendages vary in number depending on cell type and functions.

Structure-wise, the distal appendages resemble turbine blades that are symmetrically arranged at the distal end of the centriole. Here, each of the appendages is attached to one of the triplets at 50 degrees angle to centriole surface.

Unlike the distal appendage, sub-distal appendages are attached to two or three triplets and form a right angle with the centriole surface. Sub-distal appendages have also been shown to change shape/morphology and even disappear in some cases.

 

Apart from differences in shape/morphology and arrangement, distal and sub-distal appendages also have different functions. For instance, whereas the distal appendages serve to attach the centriole during cilium formation in some cells, sub-distal appendages serve as centers of nucleation for microtubules.


Central Core 


The central core is the part of a centriole on which microtubule triplets are attached. In such organisms as C. reinhardtii, this structure is about 250nm in length and has a Y-shaped linker as well as a barrel-like structure located in its inner core. As part of the centriole, the central core serves to stabilize the scaffold.


Cartwheel


The cartwheel is one of the most studied subcentriolar structures. Structure-wise, the cartwheel consists of a central hub with nine spokes/filaments radiating from it. In turn, each of these filaments/spokes is connected to the A-tubule of the microtubules through a pinhead.

The number of these structures varies between organisms and developmental stage. For instance, in Trichonympha, the number of cartwheels may vary between 7 and 10 layers during development and 2 to 4 layers when matured.

The pinhead is one of the most important structures of the cartwheel. Here, the pinhead has been shown to possess a hook-like protrusion as well as linkers located between the pinbody and microtubules. Given that the cartwheel has been shown to appear before the nine microtubules in some species, the structure is suspected to help determine the number of microtubules of a centriole.


Some of the functions of the structure have been shown to include:

 

  • Establishment of ninefold symmetry in the organelle
  • Strengthen the arrangement of triplet microtubules

 

* Microtubules in centrioles are made up of a protein known as tubulin.


A cilium (plural cilia) is an organelle found in eukaryotic cells by LadyofHats - https://commons.wikimedia.org/w/index.php?curid=3145956A cilium (plural cilia) is an organelle found in eukaryotic cells by LadyofHats - https://commons.wikimedia.org/w/index.php?curid=3145956


Centriole in Plants


Higher plants do not have centrioles. Spindle fibers that facilitate the separation of chromosomes are therefore produced by an organelle known as centrosome.

While the organelle is lacking in higher plants, it can be found in some lower plants. For instance, in such lower plants like mosses, ferns, and cycads, centrioles have been shown to form during spermatogenesis (a form of cell division).



Centriole Duplication


Like chromosomes, centrioles also duplicate once during cell division. Although it was thought that a new daughter centriole was the product of the pre-existing centriole (acting as the template for the new centriole), studies have shown following over-expression of centriolar proteins, new centrioles can be formed.

For this reason, new centrioles do not necessarily originate from pre-existing centrioles. However, in a number of scientific studies where pre-existing centrioles were completely removed, duplication was also affected. Regardless, only a single new centriole is produced with every cell cycle.

 

* New/daughter centrioles are typically assembled during the S phase of the cell cycle.


Centrosome Vs Centriole


Within a cell, centrosomes are important organelles located near the nucleus. Like centrioles, centrosomes are also absent in some multicellular organisms and some cells.

In such organisms as Drosophila, centrosomes can be seen at the poles of the spindle where they act as organizing centers of microtubules. Unlike centrioles, centrosomes have an amorphous structure. Within the centrosome are two centrioles with a well-defined structure (centrioles within the centrosome are arranged at a right angle to each other).

While the terms centriole and centrosomes do not mean the same thing, it is worth noting that the centrosome is defined by the combination of centrioles surrounded by a protein matrix known as pericentriolar material. This arrangement, however, is only observed before cell division.

During cell division, centrosomes, like centrioles, also start dividing as they move to the opposite poles of the cell.

 

** In non-dividing cells, centrioles are also involved in the formation of flagella and cilia. However, centrosomes are only involved in cell division where they form spindle apparatus.


Centriole Functions


Role of Centrioles in Cell Division


The role of centrioles in cell division is directly related to its own duplication. When new cells are produced, they contain two centrioles that start duplicating with DNA replication. When division of the cell starts, the centrosome divides into two which also results in the separation of the centrioles.

During the S phase of cell cycle, a new centriole is assembled from protein components and is referred to as a procentriole. At this stage, the centriole is not mature. During late mitosis, the juvenile centriole starts aligning at a right angle with the pre-existing centriole.

As the precentriole is aligned to the pre-existing or mother centriole, its proximal end is gradually juxtaposed to the surface of the mature centriole in a process known as engagement. This arrangement is maintained until interphase.

In combination with the protein matrix, pericentriolar material, centrioles (two mature centrioles) form the centrosomes. As cell division is about to begin, centrosomes split and start moving to the opposite poles of the cell as microtubules from each of the centrosomes gradually grow towards the central part of the cell.

During prophase, chromosomes that were duplicated during the S phase condense and become more compact. Sister chromatids are also joined together at the centromere (specialized DNA sequence) which gives them an x-shaped body. 

During the second stage of mitosis, the nuclear membrane is broken down by the phosphorylation of the nuclear lamins by kinases known as M-CDK (Cyclin-dependent kinases). This allows the spindle fibers to access the chromosomes.

As the spindle grows towards the chromosomes, they ultimately connect to the chromosomes at the centromere. Here, the microtubules (spindle microtubules) attach to a protein complex known as kinetochore assembled at the centromere. In this case, then, it's this protein complex that connects the spindle to the centromere of chromosomes.

Once the chromosomes are attached to the spindle they are pulled apart and separated. In anaphase, the sister chromatids are pulled to the opposite poles of the cell and ultimately becomes an independent chromosome.

 

* As the chromosomes are being pulled apart, there is enzymatic action on cohesin linking the chromatids that helps in the separation of the chromatids.

 

* During cell division, the proper development of centrosomes from centrioles is crucial for cell division. While cell division can occur in the absence of centrosomes in animals, the process can be messy given that the organization of microtubules takes more time. Moreover, the chromosomes may end up getting lost or in the wrong cell (Vernimmen, 2018).


See more on chromosomes.


Role of Centriole in Cilia and Flagella Formation


Apart from cell division, centrioles also play an important role in the formation of cilia and flagella. As such, they contribute to the motility of different types of cells. As well, they impart the ability of cells to sense incoming signals and respond appropriately.


Cilia and Flagella Basal Body


Essentially, cilia are composed of microtubule-based structures known as axoneme. 


There are two types of cilia that include:

 

  • Motile cilia
  • Primary cilia (non-motile cilia)

 

Whereas motile cilia have the 9+2 structure (a nine outer doublet as well as a central pair of microtubules), non-motile cilia lack this structure and is primarily involved in sensing/signal transduction that contributes to development and differentiation.

In the conversion of centrioles to basal bodies (which forms cilia) ciliary vesicles interact with the mother centriole. This results in the vesicles capping the distal end of the centriole before migrating to the surface of the cell and attaching to the plasma membrane (basal body).

The region between the basal body and axoneme is known as the transition zone. This region is characterized by axonemal doublets and Y-shaped bridges that link the microtubules to the ciliary membrane. This junction serves to determine materials that are allowed into the cilium.


Some of the accessory structures of basal bodies include:

 

  • Basal feet
  • Transition fibers
  • Ciliary rootlets 

 

* Once the basal body reaches the appropriate region on the cell, microtubules are arranged to form the axoneme. This is the basic structure (skeletal) of cilia and flagella.


* Apart from cilia and flagellum formation, centrioles have also been shown to control the direction of movement by these structures (cilia and flagellum). This makes it possible for cells to effectively move from one location to another. In cells that use cilia, cilia are aligned in a manner that allows the cell to move swiftly in a given direction.


* Despite the difference in number and length (flagella are longer and fewer in numbers compared to cilia) motile cilia and flagella have been shown to have a similar internal structure (the structure is based on the 9+2 arrangement).





Primary Cilium


In the human body, only a few cells have motile cilia. Some of these include sperm cells and ependymal cells located in brain vesicles. The majority of cells, however, have primary cilia.

Because they lack a central pair of microtubules, primary cilia are incapable of motility and are described as paralyzed in some books (meaning that they are not capable of motility). Some of these cilia do not protrude beyond the surface of the cell because they are very short.

Although primary cilia were thought to be vestigial structures by scientists, defective primary cilia have been associated with various diseases which proved that they have a role to play in the body. Based on a close examination of primary cilia on kidney tubule cells, it became evident that primary cilia act as sensors that allow cells to respond accordingly.

For instance, in the cells of kidney tubules, primary cilia were shown to be mechanoreceptors that could detect changes in the levels of calcium and thus regulate the closing and opening of calcium channels for these ions to enter the cells. At the same time, they are involved in signaling.


Take a look at Sertoli Cells

Return to page on Different Organelles

Return to Cell Theory

Return to Eukaryotic Cells

Return from Centriole page to MicroscopeMaster home






References

Erich A. Nigg and Andrew J. Holland. (2018). Once and only once: mechanisms of centriole duplication and their deregulation in disease.

 

E. Hatch and T. Stearns. (2014). The Life Cycle of Centrioles. ncbi.

 

Elif Firat-Karalar and Tim Stearns. (2014). The centriole duplication cycle. ResearchGate. 

 

LaurencePelletier. (2007). Centrioles: Duplicating Precariously. Current Biology Volume 17, Issue 17, 4 September 2007, Pages R770-R773.

 

Mark Winey and Eileen O’Toole. (2014). Centriole structure. Philosophical Transactions of the Royal Society.

 

Masafumi Hirono. (2014). Cartwheel assembly. ncbi.

 

Mike Adams. (2010). The Primary Cilium: An Orphan Organelle Finds a Home. Nature Education 3(9):54.

 

Rustem Uzbekov and Irina Alieva. (2018). Who are you, subdistal appendages of centriole? ncbi.

 

Virginie Hamel et al. (2017). Identification of Chlamydomonas Central Core Centriolar Proteins Reveals a Role for Human WDR90 in Ciliogenesis. Current Biology. 

 

 

Links 


https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3087006/

https://www.genetics.org/content/206/1/33

https://www.cell.com/current-biology/comments/S0960-9822(99)80133-X



Find out how to advertise on MicroscopeMaster!